Inferencia estadística

Intervalos de confianza con bootstrapping

Author

Edimer David Jaramillo

Published

October 24, 2024

Datos para ejemplo

Bibliotecas

Code

library(tidyverse)
library(infer)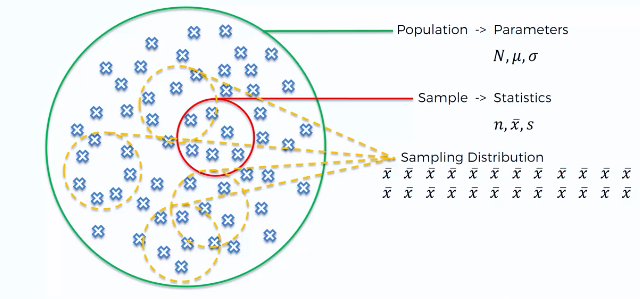

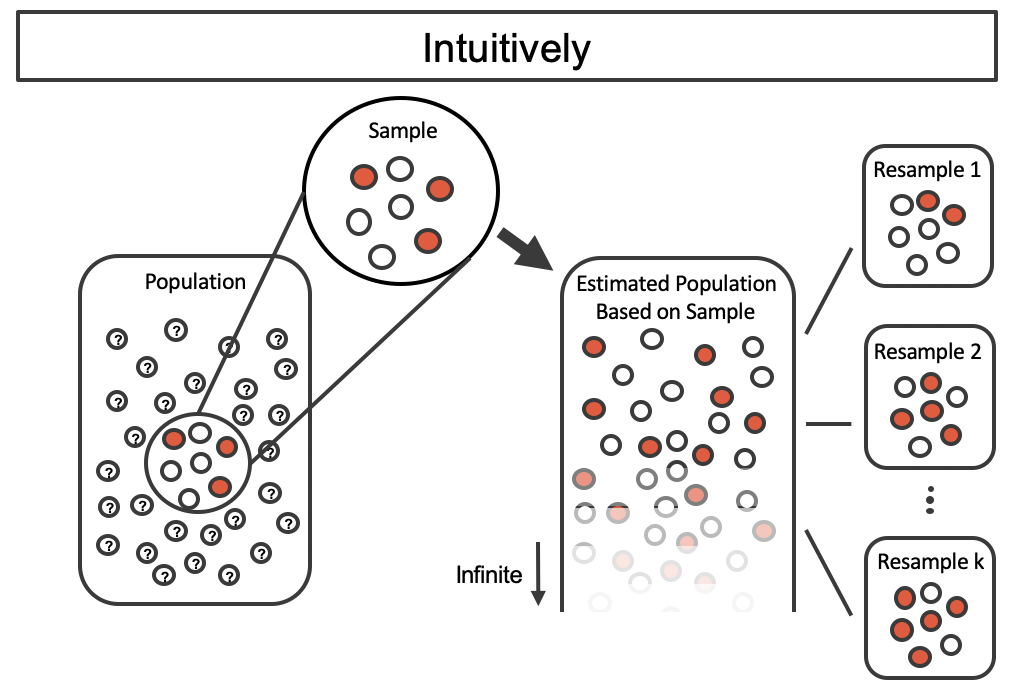
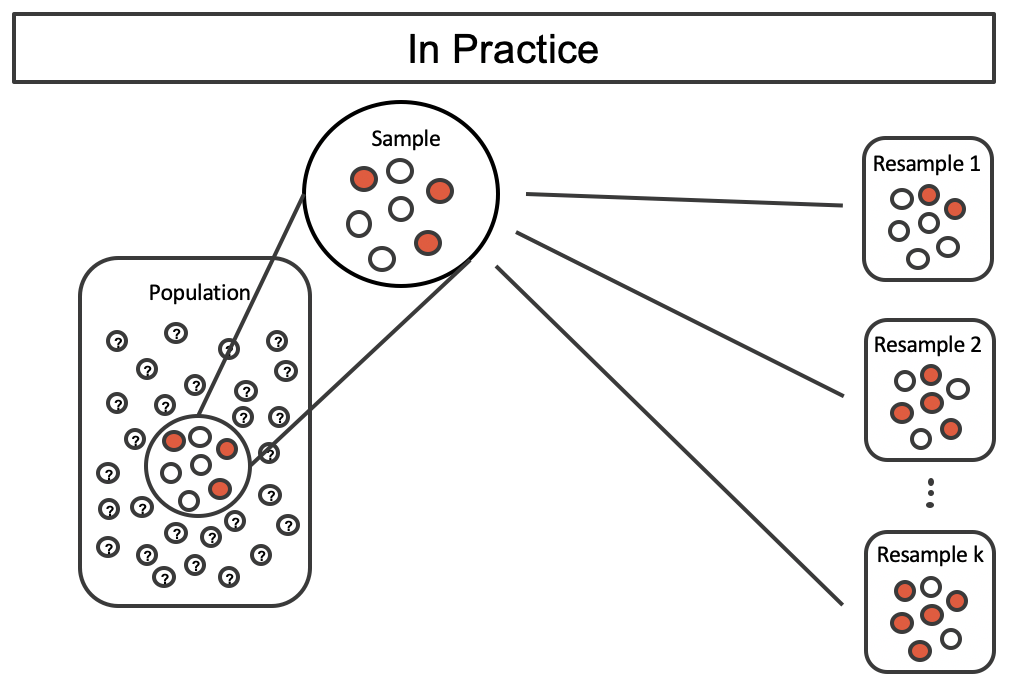
Muestreo y Bootstrapping

Fuente de imágenes: Introduction to Modern Statistics

Bibliotecas

Code

library(tidyverse)
library(infer)
library(ggpubr)

Muestreo con reemplazo

Code

set.seed(2024)
peso_tomates <- rnorm(n = 10, mean = 71.34, sd = 4.5)
sample(peso_tomates, size = 10, replace = TRUE)

 [1] 66.29392 73.44922 66.29392 76.55144 75.75886 70.85413 65.82806 75.75886
 [9] 70.76834 70.38205

Datos

Datos elecciones presidenciales

Code

datos <- read_csv("datos/EncuestasColombia2022-Update.csv")
datos |> head()

Datos encuesta

Code

df_encuesta <-
  read_csv("datos/Encuesta de clase - Diseño Experimental.csv", col_types = "cccc") |> 
  set_names(c("fecha", "prom_acad", "trabajo", "numero")) |> 
  mutate(prom_acad  = str_replace_all(prom_acad, ",", "."),
         prom_acad = as.numeric(prom_acad),
         fecha = as.POSIXct(fecha)) |> 
  filter(prom_acad <= 5)

df_encuesta |> head()

Variación del muestreo

Code

datos |> 
  ggplot(aes(x = gustavo_petro)) +
  geom_histogram(bins = 10, color = "black")

¿Cómo se distribuye la intención de voto?

Code

ggqqplot(datos$gustavo_petro)

Remuestreo (Bootstrapping)

¿Cómo cuantificar los efectos de la variación del muestreo cuando sólo tengo una muestra?

Proceso con biblioteca `infer`

1. Especificar las variables con la función specify()
1. Generar réplicas (remuestreo) con la función generate()
1. Calcular la estadísticas de resumen con la función calculate()
1. Visualice los resultados con la función visualize()
1. (opcional) Construir intervalos de confianza con la función get_confidence_interval(). Nota: para mejorar la visualización de los intervalos de confianza, se puede utilizar la función shade_confidence_interval()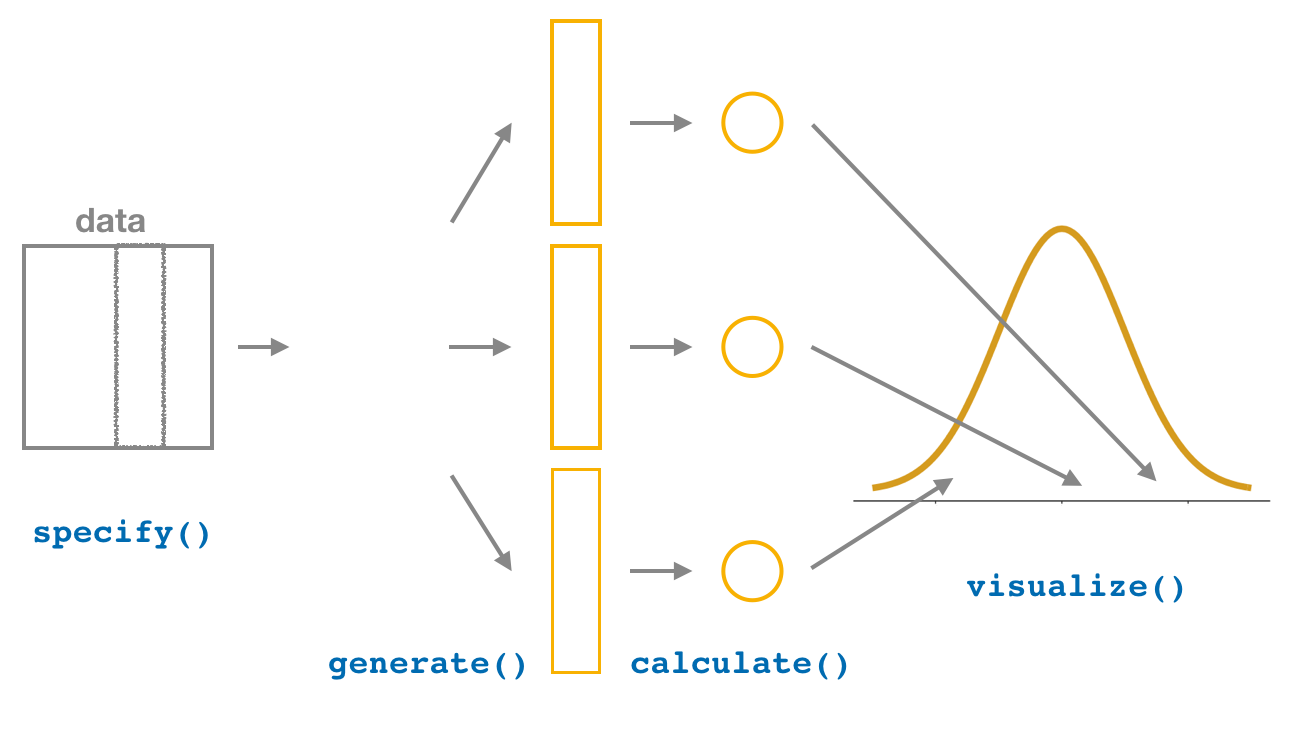

Intervalos de confianza

¿Cómo podemos construir un intervalo de confianza?
- Método 1: método del percentil
- Método 2: método del error estándar (este método se podrá implementar si y solo si la distribución bootstrapp tiene un comportamiento gaussiano)
En ambos métodos será necesaria una distribución bootstrapp y especificar un nivel de confianza.

Inferencia sobre una población

Media (\(\mu\))

En este caso vamos a estimar la media de intención de voto de un candidato “x”.

Parámetro

Code

media_muestral <- datos$gustavo_petro |>mean(na.rm = TRUE)
media_muestral

[1] 34.05121

Remuestreo - Bootstrapping

Primero obtenemos una muestra aleatoria: en este caso es el resultado de las encuestas.
Procedemos a ejecutar remuestreo para obtener la distribución bootstrap, en este caso usamos 1000 remuestreos.

Code

set.seed(2024)
remuestreo <- datos |>
  specify(response = gustavo_petro) |>
  generate(reps = 1000, type = "bootstrap") |>
  calculate(stat = "mean")

remuestreo

Graficamos la distribución bootstrap:

Code

remuestreo |>
  visualize()

Intervalo de confianza con percentiles (95%):

Code

# Usamos 0.975 porque --> 1 - 0.025 = 0.975 --> Área a la derecha
quantile(remuestreo$stat, probs = c(0.025, 0.975))

    2.5%    97.5% 
31.13422 36.87931

Code

ic_percentil <-
  remuestreo %>%
  get_confidence_interval(level = 0.95, type = "percentile")
ic_percentil

Intervalos de confianza a través del método de error estándar:

\[\bar{X} \pm z \times Error\ Estándar\]

Code

valor_z <- qnorm(p = 0.025) |> abs()

promedio_remuestreo <- mean(remuestreo$stat)
desv_remuestreo <- sd(remuestreo$stat)

lim_inferior <- promedio_remuestreo - (valor_z * desv_remuestreo)
lim_superior <- promedio_remuestreo + (valor_z * desv_remuestreo)
c(lim_inferior, lim_superior)

[1] 31.25111 36.94721

Code

ic_ee <-
  remuestreo %>%
  get_confidence_interval(level = 0.95,
                          type = "se", 
                          point_estimate = promedio_remuestreo)
ic_ee

Validamos con los resultados de la registraduría:

Code

total_votantes <- 21279308

(total_votantes * 31.13422) / 100

[1] 6625147

Code

(total_votantes * 36.87931) / 100

[1] 7847662

Graficamos el intervalo de confianza:

Code

remuestreo %>%
  visualize() +
  shade_confidence_interval(endpoints = ic_percentil) +
  geom_vline(
    xintercept = media_muestral,
    color = "red",
    lty = 2,
    size = 1.5
  ) +
  geom_vline(
    xintercept = mean(remuestreo$stat),
    color = "black",
    lty = 2,
    size = 1.5
  )

Modelo matemático (paramétrico)

\[\bar{X} - t_{\alpha/2, n-1}\frac{S}{\sqrt{n}} < \mu < \bar{X} + t_{\alpha/2, n-1}\frac{S}{\sqrt{n}}\]

Code

t.test(x = datos$gustavo_petro,
       conf.level = 0.95)


    One Sample t-test

data:  datos$gustavo_petro
t = 23.011, df = 57, p-value < 2.2e-16
alternative hypothesis: true mean is not equal to 0
95 percent confidence interval:
 31.08799 37.01442
sample estimates:
mean of x 
 34.05121

¿Cómo llegamos a este resultado manualmente?

Code

n_datos <- datos$gustavo_petro |> na.omit() |> length()
desv_muestral <- datos$gustavo_petro |> sd(na.rm = TRUE)
estadistico_t <- qt(p = 0.025, df = n_datos-1) |> abs()


media_muestral - (estadistico_t * (desv_muestral / sqrt(n_datos) ) )

[1] 31.08799

Code

media_muestral + (estadistico_t * (desv_muestral / sqrt(n_datos) ) )

[1] 37.01442

Proporción (\(p\))

Proporción muestral

Proporción de estudiantes que tienen trabajo remunerado:

Code

df_encuesta$trabajo |> 
  table() |> 
  prop.table()


       No        Sí 
0.6129032 0.3870968

Remuestreo - Bootstrapping

¿Cuál es la verdadera proporción de estudiantes que tienen trabajo remunerado?

Code

set.seed(2024)
remuestreo_trabajo <- df_encuesta %>%
  specify(response = trabajo, success = "Sí") %>%
  generate(reps = 1000, type = "bootstrap") %>%
  calculate(stat = "prop")

remuestreo_trabajo

Graficamos la distribución del remuestreo:

Code

remuestreo_trabajo |> 
  visualize()

Calculamos el intervalo de confianza por el método de percentiles:

Code

ic_perc_trabajo <-
  remuestreo_trabajo %>%
  get_confidence_interval(level = 0.95, type = "percentile")
ic_perc_trabajo

Graficamos los intervalos de confianza con el método de percentiles:

Code

remuestreo_trabajo |>
  visualize() +
  shade_confidence_interval(endpoints = ic_perc_trabajo)

Modelo matemático (paramétrico)

\[\hat{p}-Z_{\alpha/2}\sqrt{\frac{\hat{p}(1-\hat{p})}{n}} < p < \hat{p}+Z_{\alpha/2}\sqrt{\frac{\hat{p}(1-\hat{p})}{n}}\]

Conteo:

Code

df_encuesta |> 
  count(trabajo)

Ahora aplicamos la prueba estadística para proporciones:

Code

total_muestra <- df_encuesta |> nrow()
total_trabajo <- 12
proporcion_referencia <- 0.5
prop.test(x = total_trabajo, n = total_muestra, p = proporcion_referencia)


    1-sample proportions test with continuity correction

data:  total_trabajo out of total_muestra, null probability proporcion_referencia
X-squared = 1.1613, df = 1, p-value = 0.2812
alternative hypothesis: true p is not equal to 0.5
95 percent confidence interval:
 0.2241645 0.5771290
sample estimates:
        p 
0.3870968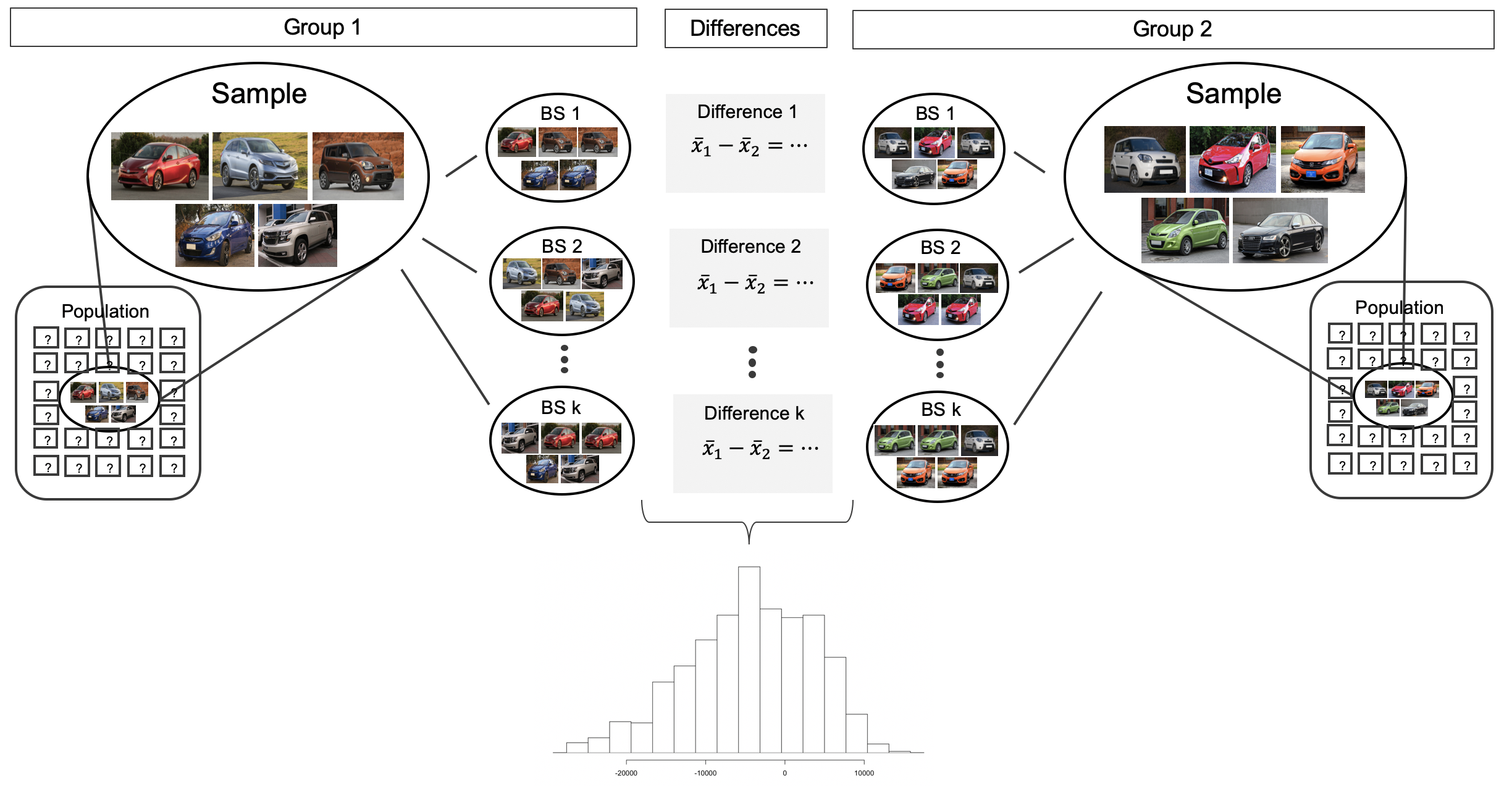

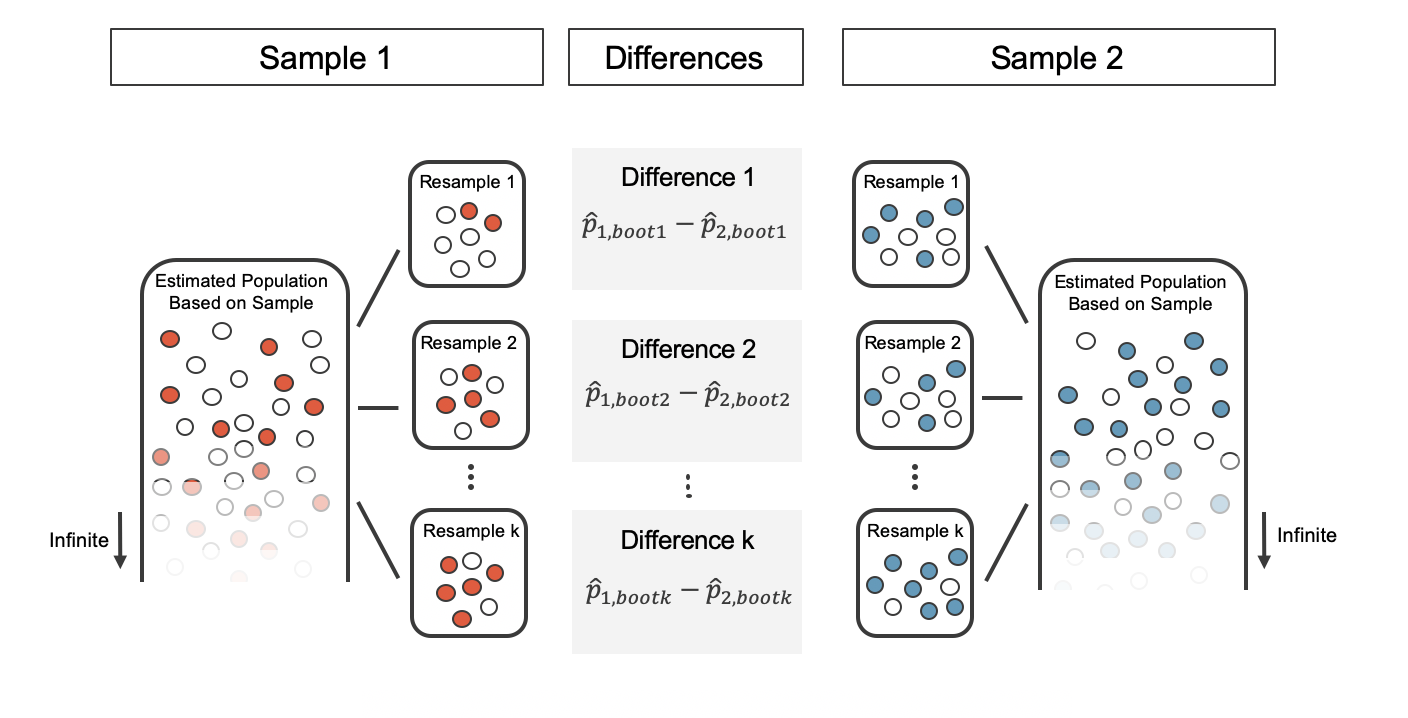
Inferencia sobre 2 poblaciones

Inferencia sobre \(\mu_1 - \mu_2\)

Para este ejemplo nos preguntamos si el promedio académico de los y las estudiantes que poseen trabajo es superior o inferior a los que no trabajan.

Medias muestrales

Code

medias_muestrales <-
  df_encuesta |> 
  group_by(trabajo) |> 
  reframe(promedio = mean(prom_acad))

medias_muestrales

Diferencia de medias muestrales

Ahora calculamos la diferencia (parámetro de interés) de las medias muestrales

Code

media_no <- medias_muestrales |> filter(trabajo == "No") |> pull(promedio)
media_si <- medias_muestrales |> filter(trabajo == "Sí") |> pull(promedio)

diferencia_muestral <- media_si - media_no
diferencia_muestral

[1] 0.01890351

¿Es estadísticamente significativa esta diferencia? 🤔

Remuestreo - Bootstrapping

Code

set.seed(2024)
remuestreo_dif_medias <- df_encuesta |>
  specify(formula = prom_acad ~ trabajo) |>
  generate(reps = 1000, type = "bootstrap") |>
  calculate(stat = "diff in means", order = c("Sí", "No"))

remuestreo_dif_medias

Graficamos la distribución bootstrap:

Code

remuestreo_dif_medias |> 
  visualize()

Ahora obtenemos el intervalo de confianza con el método de percentiles:

Code

ic_dif_medias <-
  remuestreo_dif_medias |> 
  get_confidence_interval(level = 0.95,
                          type = "percentile")

ic_dif_medias

Graficamos el intervalo de confianza para la diferencia de medias:

Code

remuestreo_dif_medias %>%
  visualize() +
  shade_confidence_interval(endpoints = ic_dif_medias) +
  geom_vline(
    xintercept = diferencia_muestral,
    color = "red",
    lty = 2,
    size = 1.5
  ) +
  geom_vline(
    xintercept = mean(remuestreo_dif_medias$stat),
    color = "black",
    lty = 2,
    size = 1.5
  )

Modelo matemático (paramétrico)

Code

t.test(df_encuesta$prom_acad ~ df_encuesta$trabajo,
       mu = 0,
       conf.level = 0.95)


    Welch Two Sample t-test

data:  df_encuesta$prom_acad by df_encuesta$trabajo
t = -0.19683, df = 21.603, p-value = 0.8458
alternative hypothesis: true difference in means between group No and group Sí is not equal to 0
95 percent confidence interval:
 -0.218288  0.180481
sample estimates:
mean in group No mean in group Sí 
        3.985263         4.004167

Preguntas finales

¿Por qué nuestras estimaciones puntuales difieren del parámetro poblacional?
¿Es conveniente utilizar intervalos de confianza?

Exactitud vs Precisión

Fuente: Statistical Inference via Data Science

Intervalos de confianza: Idea intuitiva

Fuente: Statistical Inference via Data Science

Anexo

Distribución normal estándar

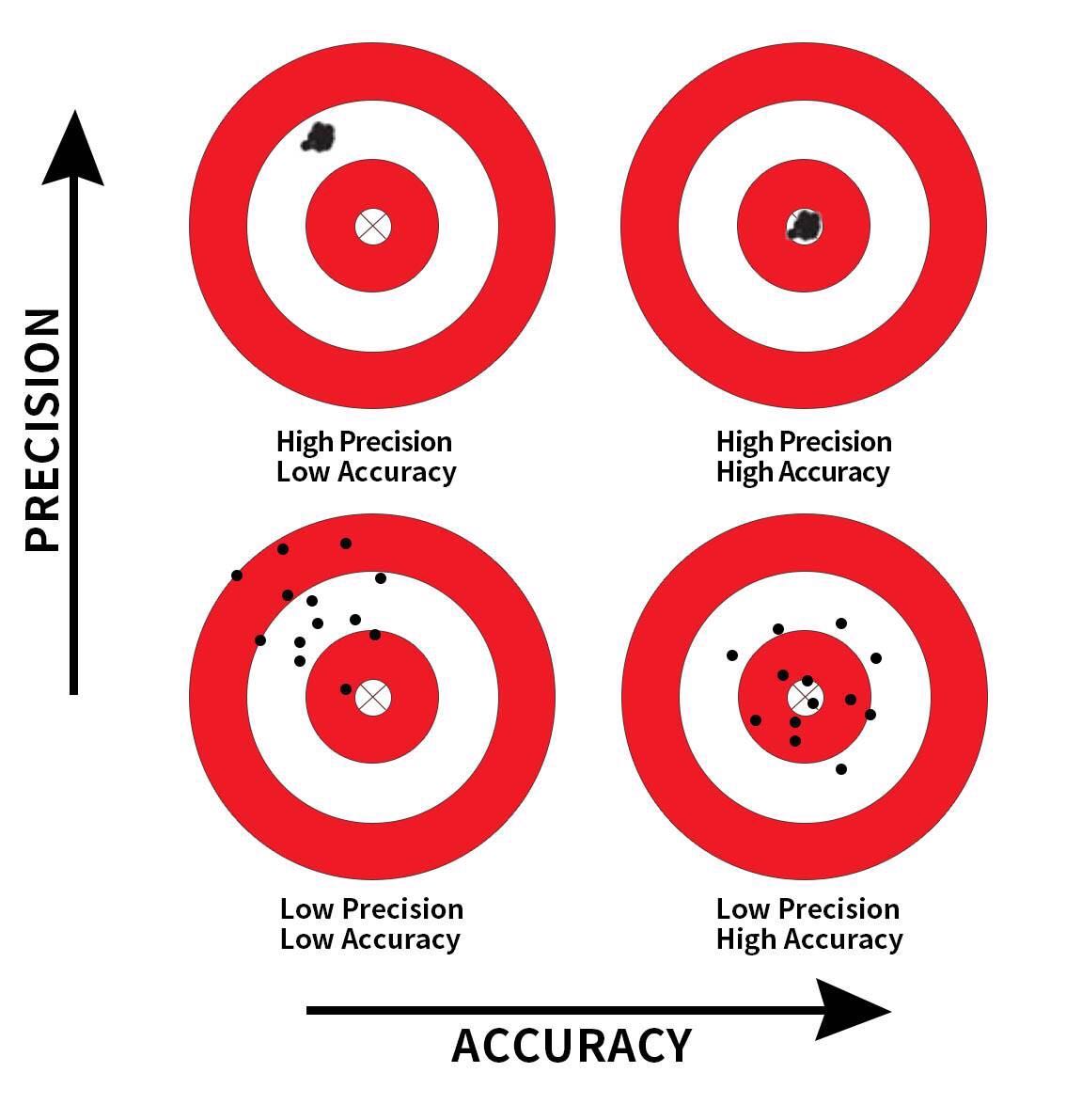
\[z = \frac{x - \mu}{\sigma}\]

Promedio académico:

Code

media_prom <- df_encuesta$prom_acad |> mean()
desv_prom <- df_encuesta$prom_acad |> sd()

(df_encuesta$prom_acad - media_prom) / desv_prom

 [1]  0.02969807 -0.77085856 -2.37197180 -0.37058024  0.42997638 -0.77085856
 [7]  0.02969807 -1.17113687  0.02969807  0.42997638  0.83025469  0.83025469
[13] -0.37058024  1.63081132 -0.77085856  0.83025469 -0.37058024  0.02969807
[19] -1.17113687 -0.37058024  0.02969807  0.02969807  0.42997638 -0.29052458
[25] -0.77085856  0.79022686  1.63081132  2.03108963  0.83025469 -2.13180481
[31]  0.83025469

¿Cuál es la probabilidad de que al tomar un estudiante al azar su promedio académico sea mayor a 4.1?

Code

valor_z <- (4.1 - media_prom) / desv_prom

Calculando la probabilidad con la distribución normal estándar:

Code

1 - pnorm(q = valor_z, mean = 0, sd = 1)

[1] 0.3336064

Podemos calcular la probabilidad directamente con los valores originales:

Code

1 - pnorm(q = 4.1, mean = media_prom, sd = desv_prom)

[1] 0.3336064

Intención de voto:

Code

media_voto <- datos$gustavo_petro |> mean(na.rm = TRUE)
desv_voto <- datos$gustavo_petro |> sd(na.rm = TRUE)

(datos$gustavo_petro - media_voto) / desv_voto

 [1]  0.527857982  0.980399474  0.341517367  0.616591608  0.155176753
 [6]  0.947568032  0.581098157  0.350390730  0.229712999  0.527857982
[11]  0.208416929  0.847299035  0.350390730  0.758565409 -0.004543774
[16] -0.004543774  0.217290291 -0.182011025  0.261657104  0.936032661
[21]  0.714198596  0.101936577 -0.119897487 -0.528072166 -0.625679155
[26] -0.625679155 -0.803146407 -0.767652956 -1.069347284 -0.714412781
[31] -1.273434624 -1.513015414 -1.104840735 -0.341731552 -1.158080910
[36] -0.332858189 -1.193574361 -0.803146407 -0.874133307  0.377010818
[41] -0.980613658 -1.335548162 -0.723286143 -1.832456467 -1.601749040
[46] -1.557382227 -0.279618014 -1.424281788 -0.102150762  1.104626550
[51]           NA  1.424067603  2.107316523  1.991962809           NA
[56]           NA  1.654775031  1.628154943  0.572224795           NA
[61]  1.415194241  1.947595996           NA           NA           NA

¿Cuál era la probabilidad de que el candidato obtuviera más del 50% de los votos?

Code

1 - pnorm(q = 50, mean = media_voto, sd = desv_voto)

[1] 0.07850578

Datos para ejemplo

Bibliotecas

Muestreo y Bootstrapping

Bibliotecas

Muestreo con reemplazo

Datos

Datos elecciones presidenciales

Datos encuesta

Variación del muestreo

Remuestreo (Bootstrapping)

Proceso con biblioteca infer

Intervalos de confianza

Inferencia sobre una población

Media (\(\mu\))

Parámetro

Remuestreo - Bootstrapping

Modelo matemático (paramétrico)

Proporción (\(p\))

Proporción muestral

Remuestreo - Bootstrapping

Modelo matemático (paramétrico)

Inferencia sobre 2 poblaciones

Inferencia sobre \(\mu_1 - \mu_2\)

Medias muestrales

Diferencia de medias muestrales

Remuestreo - Bootstrapping

Modelo matemático (paramétrico)

Preguntas finales

Exactitud vs Precisión

Intervalos de confianza: Idea intuitiva

Anexo

Distribución normal estándar

Proceso con biblioteca `infer`