Diseño Experimental

Autor/a

Edimer David Jaramillo

Fecha de publicación

18 de abril de 2024

Bibliotecas

Código 
library(tidyverse)
library(readxl)
library(infer)

theme_set(theme_bw())

Datos

Código 
datos <- read_excel("datos/datos-encuestas-historia.xlsx")
datos

Escenarios de inferencia

Hipótesis estadística

Tipos de pruebas

Tipos de errores

Inferencia sobre una población

Inferencia sobre la media

Normalidad de la variable

Código 
ggpubr::ggqqplot(datos$promedio_acad)

Juego de hipótesis

\[H_0: \mu = 3.5\]

\[H_1: \mu \neq 3.5\]

Nivel de significancia

  • Vamos a utilizar un nivel de significancia del 5% (\(\alpha = 0.05\))

Calcular el estadístico observado

  • En este caso calculamos el estadístico T:

\[T = \frac{\bar{X} - \mu}{S/\sqrt{n}}\]

Código 
x_barra <- mean(datos$promedio_acad, na.rm = TRUE)
mu_referencia <- 3.5
desviacion_muestral <- sd(datos$promedio_acad, na.rm = TRUE)
raiz_n <- sqrt(nrow(datos))

\[T = \frac{3.794516 - 3.5}{0.247371/9.643651} = 11.48158\]

Código 
(x_barra - mu_referencia) / (desviacion_muestral / raiz_n)
[1] 11.48158

Región de rechazo

Código 
qt(p = 0.025, df = 92, lower.tail = TRUE)
[1] -1.986086
Código 
qt(p = 0.025, df = 92, lower.tail = FALSE)
[1] 1.986086

  • Conclusión: como el estadístico calculado (11.48158) está dentro de las regiones de rechazo, existe evidencia para rechazar la hipótesis nula, es decir, que se rechaza que el promedio del promedio_académico sea igual a 3.5. Esto se concluye con un nivel de significancia del 5%.

Intervalo de confianza para \(\mu\)

  • Límite inferior del intervalo de confianza:

\[\bar{X} - t_{\alpha/2, n-1} \times \frac{s}{\sqrt{n}}\]

Código 
x_barra - (1.986086 * (desviacion_muestral / raiz_n))
[1] 3.743571
  • Límite superior del intervalo de confianza:

\[\bar{X} + t_{\alpha/2, n-1} \times \frac{s}{\sqrt{n}}\]

Código 
x_barra + (1.986086 * (desviacion_muestral / raiz_n))
[1] 3.845462
  • Conclusión: como el valor de referencia (3.5) no está dentro del intervalo de confianza, existe evidencia para rechazar la hipótesis nula, es decir, que se rechaza que el promedio del promedio_académico sea igual a 3.5. Esto se concluye con un nivel de significancia del 5%. Como el intervalo de confianza está a la derecha del valor de referencia (3.5) podemos afirmar que la media del promedio académico de los estudiantes es mayor a 3.5

Valor p

  • Calcular el área que deja un valor de 11.48158 a la izquierda:
Código 
pt(q = -11.48158, df = 92, lower.tail = TRUE)
[1] 9.287894e-20
  • Calcular el área que deja un valor de 11.48158 a la derecha:
Código 
pt(q = 11.48158, df = 92, lower.tail = FALSE)
[1] 9.287894e-20
  • El valor p es la suma de las dor áreas anteriores:
Código 
9.287894e-20 + 9.287894e-20
[1] 1.857579e-19
  • Conclusión: como el valor p (1.857579e-19) es menor que el nivel de significancia (0.05) existe evidencia para rechazar la hipótesis nula.

Solución con R

  • Utilizamos la función t.test() con los siguientes argumentos:
    • x: la variable sobre la cual estamos haciendo inferencia. En este caso el promedio_académico
    • alternative: tipo de hipótesis alternativa. En este es una prueba bilateral usamos “two.sided”
    • conf.level: nivel de confianza (1 - nivel de significancia = 1 - 0.05 = 0.95)
    • mu: valor promedio de referencia. En este caso es 3.5
Código 
t.test(x = datos$promedio_acad,
       alternative = "two.sided",
       conf.level = 0.95,
       mu = 3.5)

    One Sample t-test

data:  datos$promedio_acad
t = 11.482, df = 92, p-value < 2.2e-16
alternative hypothesis: true mean is not equal to 3.5
95 percent confidence interval:
 3.743571 3.845462
sample estimates:
mean of x 
 3.794516
  • Presentando resultados de la prueba anterior, de forma ordenada (tidy):
Código 
prueba_t1 <- t.test(
  x = datos$promedio_acad,
  alternative = "two.sided",
  conf.level = 0.95,
  mu = 3.5
)

library(broom)
prueba_t1 |> tidy()

Alternativa no parámetrica 1: Test de Wilcoxon

Código 
wilcox.test(
  x = datos$promedio_acad,
  alternative = "two.sided",
  conf.int = TRUE,
  conf.level = 0.95,
  mu = 3.5
)

    Wilcoxon signed rank test with continuity correction

data:  datos$promedio_acad
V = 3465.5, p-value = 6.357e-14
alternative hypothesis: true location is not equal to 3.5
95 percent confidence interval:
 3.794980 3.884976
sample estimates:
(pseudo)median 
       3.84006

Alternativa no parámetrica 2: Bootstrapping

Muestreo

Código 
ejemplo <- c(45, 32.5, 85.3, 74.3, 110, 26.8, 28.6)

set.seed(2024)
remuestreo1 <- sample(ejemplo, size = 100, replace = TRUE)
remuestreo2 <- sample(ejemplo, size = 100, replace = TRUE)
remuestreo3 <- sample(ejemplo, size = 100, replace = TRUE)
remuestreo4 <- sample(ejemplo, size = 100, replace = TRUE)
remuestreo5 <- sample(ejemplo, size = 100, replace = TRUE)
remuestreo6 <- sample(ejemplo, size = 100, replace = TRUE)
remuestreo7 <- sample(ejemplo, size = 100, replace = TRUE)
remuestreo8 <- sample(ejemplo, size = 100, replace = TRUE)
remuestreo9 <- sample(ejemplo, size = 100, replace = TRUE)
remuestreo10 <- sample(ejemplo, size = 100, replace = TRUE)
  • Calculamos el promedio de la muestra original:
Código 
mean(ejemplo)
[1] 57.5
  • Calculamos el promedio de cada remuestreo:
Código 
prom_r1 <- mean(remuestreo1)
prom_r2 <- mean(remuestreo2)
prom_r3 <- mean(remuestreo3)
prom_r4 <- mean(remuestreo4)
prom_r5 <- mean(remuestreo5)
prom_r6 <- mean(remuestreo6)
prom_r7 <- mean(remuestreo7)
prom_r8 <- mean(remuestreo8)
prom_r9 <- mean(remuestreo9)
prom_r10 <- mean(remuestreo10)

vector_promedios <- c(prom_r1, prom_r2, prom_r3, prom_r4, prom_r5,
                      prom_r6, prom_r7, prom_r8, prom_r9, prom_r10)

promedio_remuestreos <- mean(vector_promedios)

ggplot(mapping = aes(x = vector_promedios)) +
  geom_density() +
  geom_vline(xintercept = promedio_remuestreos, color = "red")

Boootstrapping

Código 
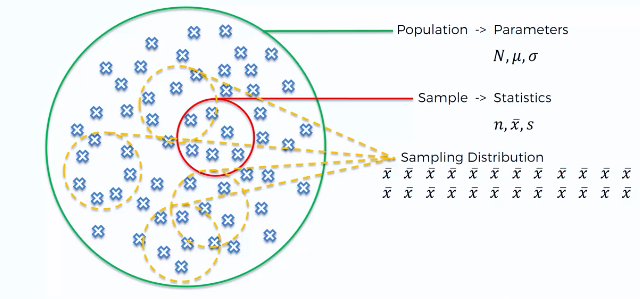
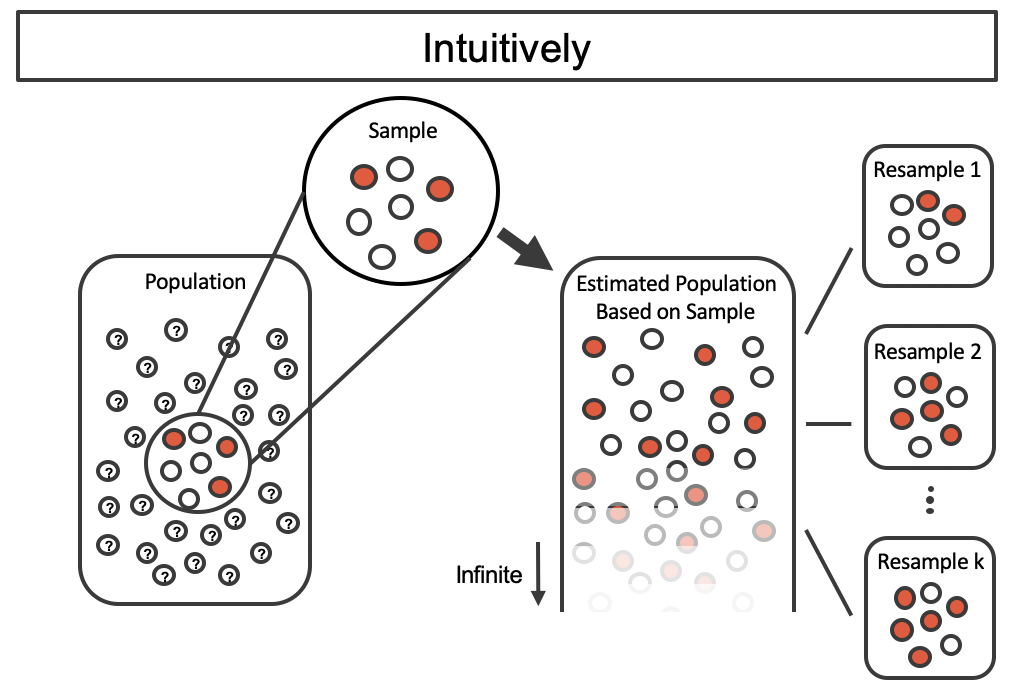
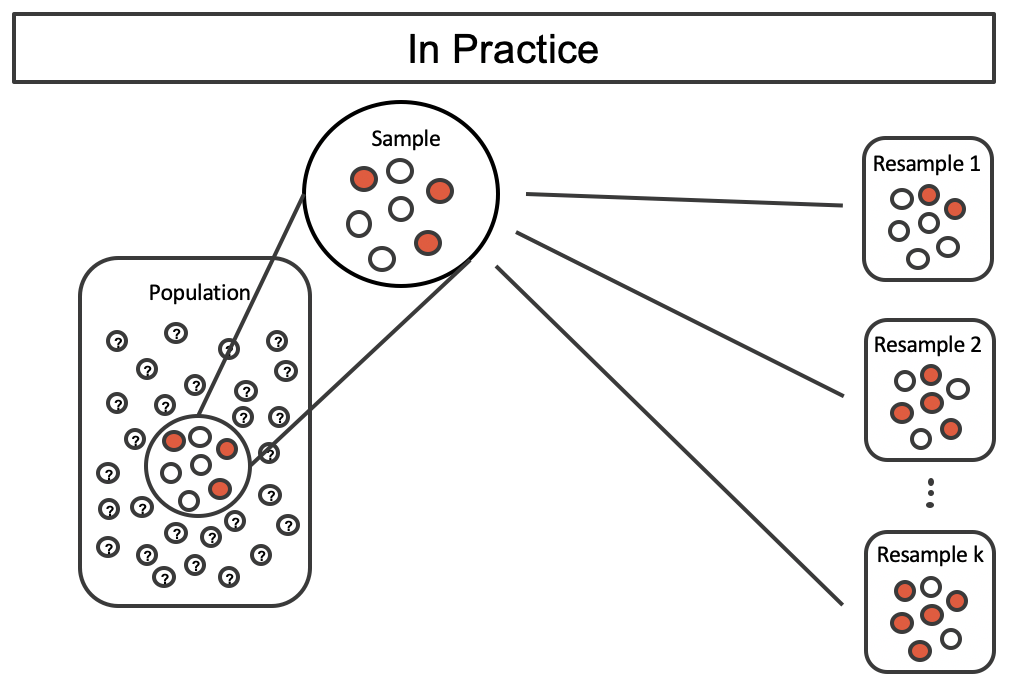
ejemplo <- c(45.67, 67.87, 65, 70, 110, 35.7)

sample(ejemplo, size = 7, replace = TRUE)
[1]  45.67 110.00  70.00  45.67  35.70  70.00  45.67

Proceso con biblioteca infer

    1. Especificar las variables con la función specify()
    1. Generar réplicas (remuestreo) con la función generate()
    1. Calcular la estadísticas de resumen con la función calculate()
    1. Visualice los resultados con la función visualize()
    1. (opcional) Construir intervalos de confianza con la función get_confidence_interval(). Nota: para mejorar la visualización de los intervalos de confianza, se puede utilizar la función shade_confidence_interval()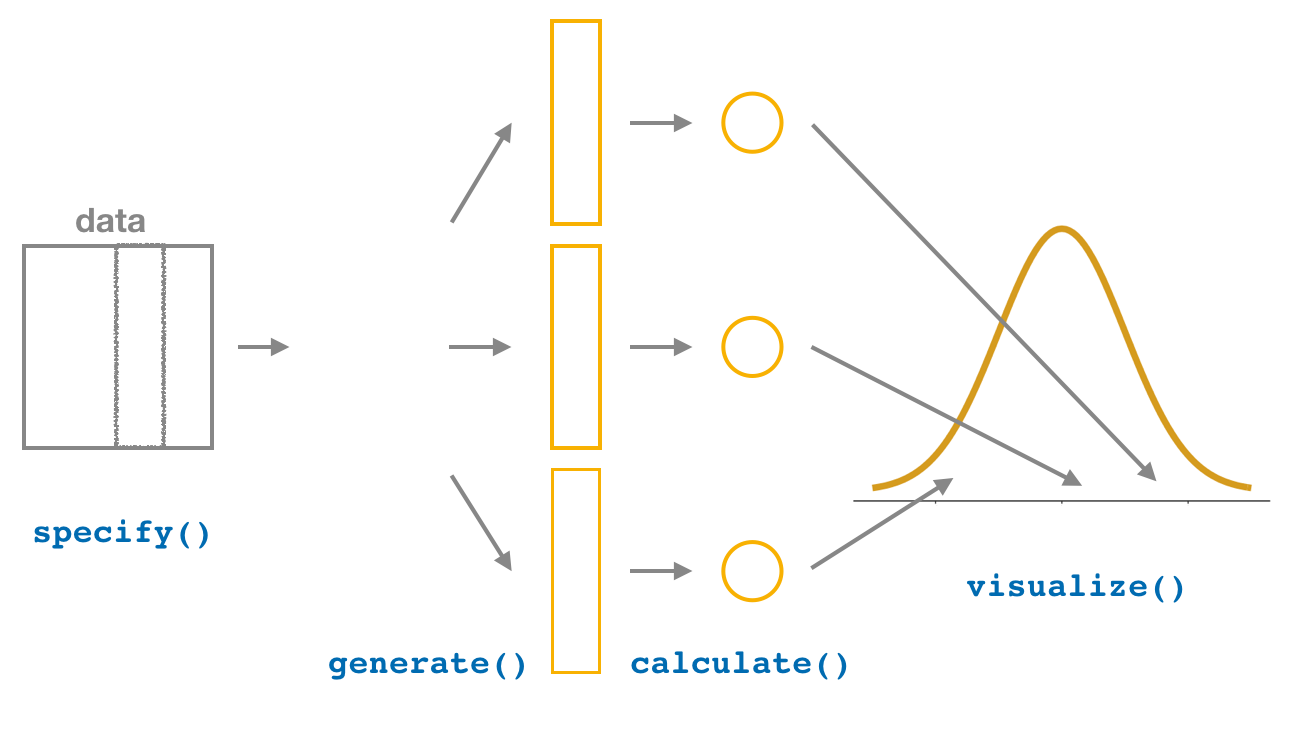

Código 
set.seed(2024)
bootstrap_promedio_udea <- 
  datos |> 
  specify(response = promedio_acad) |> 
  generate(reps = 1000, type = "bootstrap") |> 
  calculate(stat = "mean")

bootstrap_promedio_udea
  • Graficamos la distribución bootstrap:
Código 
bootstrap_promedio_udea |> 
  visualize()

Intervalos de confianza

{fig-align=“center” width = “70%”}

Método de percentiles

  • Intervalo de confianza con percentiles (95%):
Código 
ic_promedio_percentil <-
  bootstrap_promedio_udea |> 
  get_confidence_interval(level = 0.95, type = "percentile")
ic_promedio_percentil
  • Graficamos el intervalo de confianza obtenido con el método de percentiles:
Código 
bootstrap_promedio_udea |> 
  visualize() +
  shade_confidence_interval(endpoints = ic_promedio_percentil) +
  geom_vline(
    xintercept = x_barra,
    color = "red",
    lty = 2,
    size = 1.5
  ) +
  geom_vline(
    xintercept = mean(datos$promedio_acad),
    color = "black",
    lty = 2,
    size = 1.5
  )

Método de error estándar

  • Intervalo de confianza con método del error estándar:
Código 
ic_promedio_error_est <-
  bootstrap_promedio_udea |> 
  get_confidence_interval(type = "se", point_estimate = x_barra)
ic_promedio_error_est
  • Graficamos el intervalo de confianza obtenido con el método de percentiles:
Código 
bootstrap_promedio_udea |> 
  visualize() +
  shade_confidence_interval(endpoints = ic_promedio_error_est) +
  geom_vline(
    xintercept = x_barra,
    color = "red",
    lty = 2,
    size = 1.5
  ) +
  geom_vline(
    xintercept = mean(datos$promedio_acad),
    color = "black",
    lty = 2,
    size = 1.5
  )

:::

Referencia